Neural Networks Implementation

First we import the necessary libraries

import torch as t
import matplotlib.pyplot as plt
%matplotlib inline
# Retina 
%config InlineBackend.figure_format = 'retina'

Here we define the dataset to use.

x - a collection of numbers between 0 and 10 with a step of 0.1

f - a function that we will use to generate the y values

y - a collection of y values generated from the x values using the function f and adding some noise (t.randn(len(x), 1))

x = t.arange(0, 100, 0.1, dtype=t.float32).reshape(-1, 1)

def f(x):
    return 4 + 3 * x

f_vals = f(x)
eps = t.randn(len(x), 1)

y = f_vals + eps

def normalize(x):
    mean = x.mean()
    std = x.std()
    return (x - mean) / std, mean, std

def denormalize(x, mean, std):
    return x * std + mean

Define a function to plot the data for visualisation

x.shape, y.shape, f_vals.shape

(torch.Size([1000, 1]), torch.Size([1000, 1]), torch.Size([1000, 1]))

plt.scatter(x.ravel(), y.ravel(), label='data')
plt.plot(x.ravel(), f_vals.ravel(), color='red', label='True function')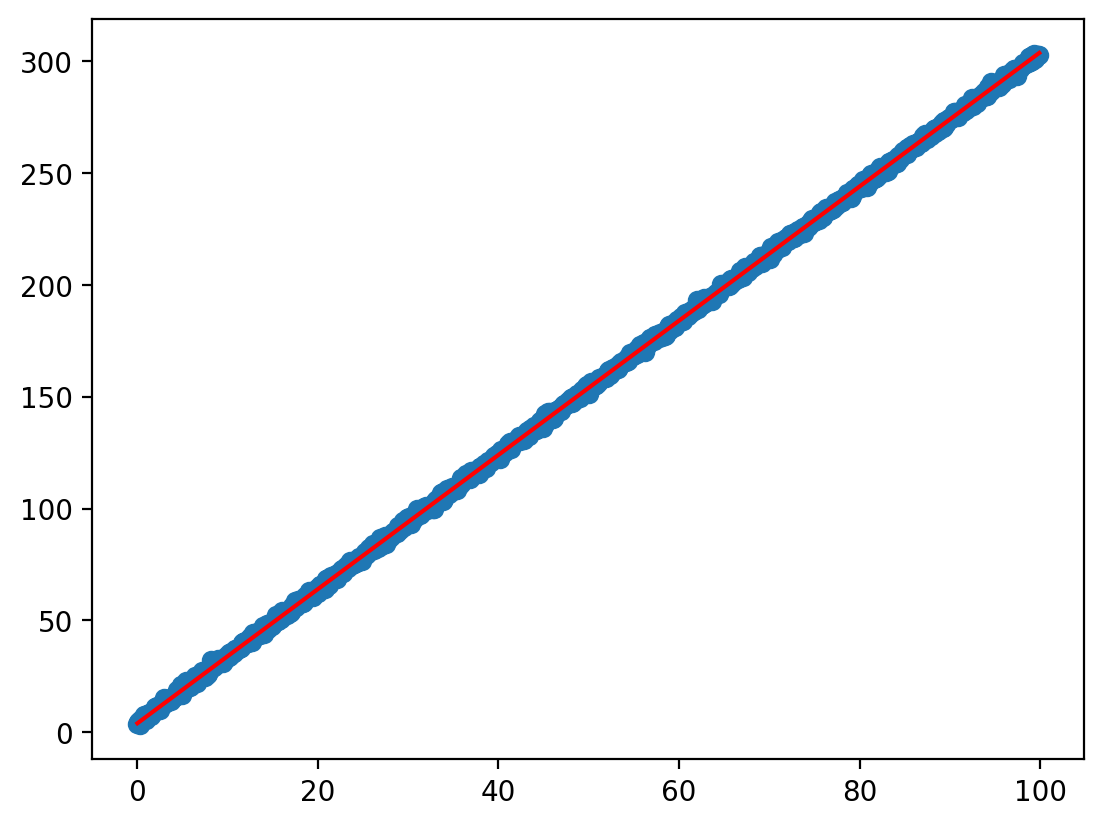

def graph(y_hat):
    """
    This is a function to graph the data
    y_hat - tensor of the predicted values by training
    """
    plt.scatter(x, y, label='data')
    plt.plot(x, f_vals, color='red', label='True function')
    plt.plot(x, y_hat.detach().numpy(), color='green', label='Pred')
    plt.legend()

Define the loss function

def loss_function(y, y_hat):
    """
    This is a function to calculate the loss with "Mean Squared Error"
    y - tensor of the actual values
    y_a - tensor of the predicted values
    """
    return t.mean(t.square(y - y_hat))

Version 1

Define the neural network weights and biases

w11 = t.randn(1, requires_grad=True)
w12 = t.randn(1, requires_grad=True)
w21 = t.randn(1, requires_grad=True)
w22 = t.randn(1, requires_grad=True)

b11 = t.randn(1, requires_grad=True)
b12 = t.randn(1, requires_grad=True)
b21 = t.randn(1, requires_grad=True)
b22 = t.randn(1, requires_grad=True)

The training loop

losses = []

lr = 0.0001

for i in range(5000):
    z1 = (w11 * x + b11)
    a1 = t.relu(z1)
    z2 = (w12 * x + b12)
    a2 = t.relu(z2)

    y_hat = ((w21 * a1 + b21) + (w22 * a2 + b22))
    
    l = loss_function(y, y_hat)

    if i % 100 == 0:
        print(f"{i} loss: {l}")

    losses.append(l.item())

    l.backward()
    
    with t.no_grad(): 
        w11.data = w11.data - lr * w11.grad
        w12.data = w12.data - lr * w12.grad
        w21.data = w21.data - lr * w21.grad
        w22.data = w22.data - lr * w22.grad

        b11.data = b11.data - lr * b11.grad
        b12.data = b12.data - lr * b12.grad
        b21.data = b21.data - lr * b21.grad
        b22.data = b22.data - lr * b22.grad

        w11.grad = None
        w12.grad = None
        w21.grad = None
        w22.grad = None

        b11.grad = None
        b12.grad = None
        b21.grad = None
        b22.grad = None

0 loss: 7688.90185546875
100 loss: 7674.01513671875
200 loss: 7660.27197265625
300 loss: 7647.58544921875
400 loss: 7635.8740234375
500 loss: 7625.0625
600 loss: 7615.08203125
700 loss: 7605.8681640625
800 loss: 7597.36279296875
900 loss: 7589.5107421875
1000 loss: 7582.26220703125
1100 loss: 7575.57080078125
1200 loss: 7569.39208984375
1300 loss: 7563.68896484375
1400 loss: 7558.423828125
1500 loss: 7553.56298828125
1600 loss: 7549.07568359375
1700 loss: 7544.9326171875
1800 loss: 7541.10693359375
1900 loss: 7537.576171875
2000 loss: 7534.31591796875
2100 loss: 7531.30615234375
2200 loss: 7528.52685546875
2300 loss: 7525.96044921875
2400 loss: 7523.59130859375
2500 loss: 7521.4033203125
2600 loss: 7519.38427734375
2700 loss: 7517.52001953125
2800 loss: 7515.796875
2900 loss: 7514.2060546875
3000 loss: 7512.73779296875
3100 loss: 7511.380859375
3200 loss: 7510.1279296875
3300 loss: 7508.97119140625
3400 loss: 7507.90234375
3500 loss: 7506.916015625
3600 loss: 7506.00341796875
3700 loss: 7505.1611328125
3800 loss: 7504.38232421875
3900 loss: 7503.66357421875
4000 loss: 7502.998046875
4100 loss: 7502.3837890625
4200 loss: 7501.81640625
4300 loss: 7501.29150390625
4400 loss: 7500.8056640625
4500 loss: 7500.35693359375
4600 loss: 7499.9423828125
4700 loss: 7499.55810546875
4800 loss: 7499.20263671875
4900 loss: 7498.87353515625

Plot the losses to see how the model is learning

plt.plot(losses)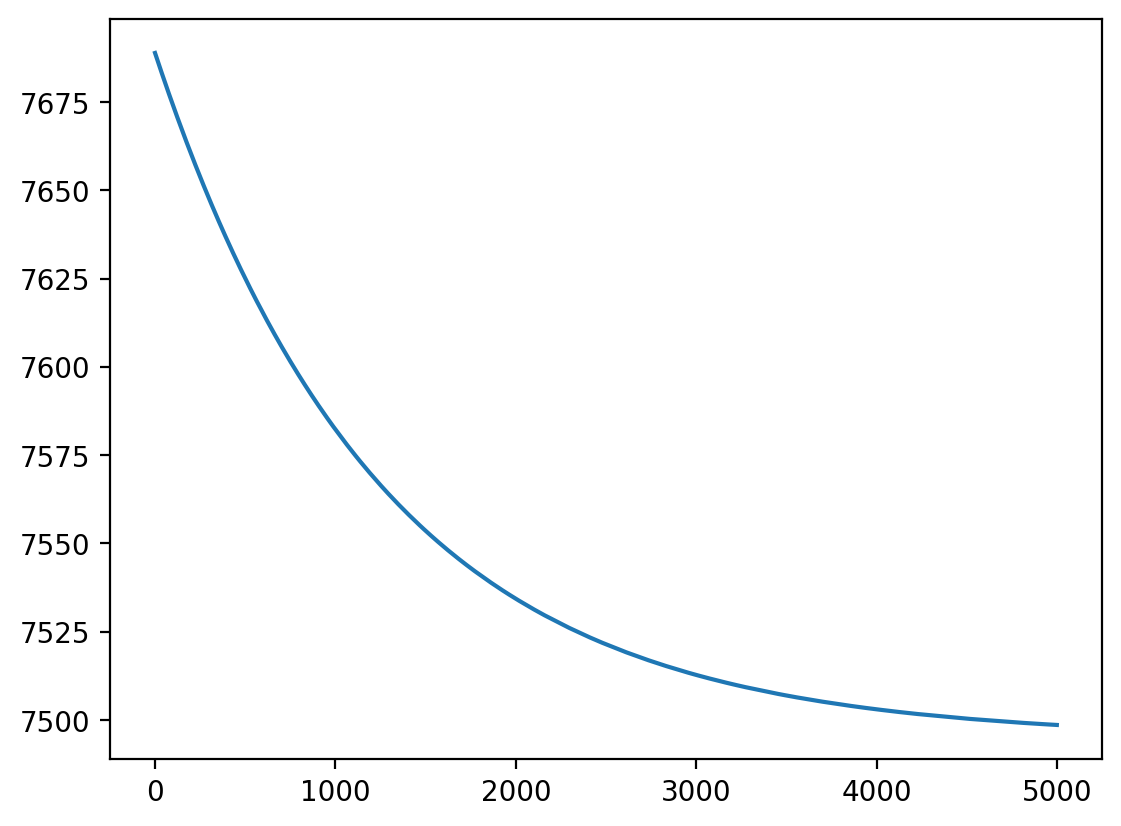

Plot the model predictions against the actual data and the function used to generate the data

graph(y_hat)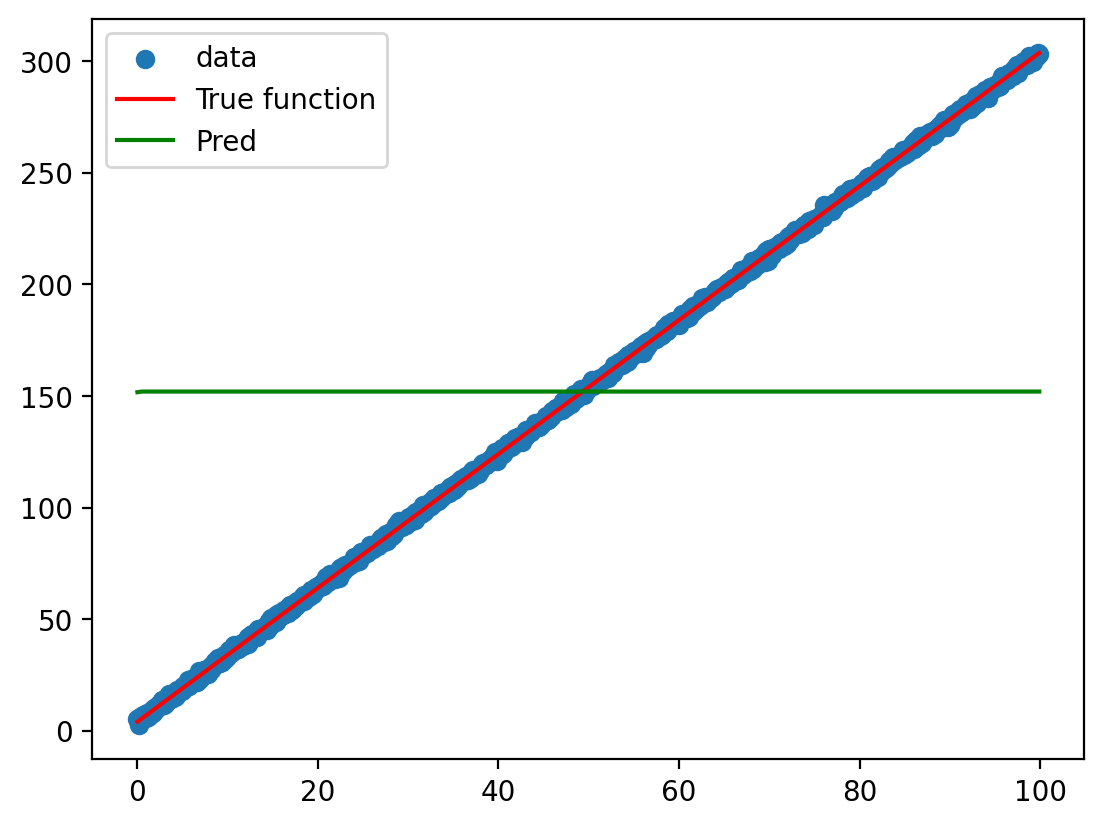

Version 2

Define a function to initialise the weights and biases of the neural network by giving the total number of weights required

def init(weights_no):
    """
    This is a function to initialize the weights and biases
    weights_no - total number of weights required (exclusive of biases)
    """
    weights = []

    for _ in range(weights_no):
        weights.append(t.randn(1, requires_grad=True))
        weights.append(t.randn(1, requires_grad=True))
    
    return weights

Define a forward propagation function to calculate the predictions of the neural network

def forward(x, w11, w12, w21, w22, b11, b12, b21, b22):
    """
    This is a function for forward propagation of the neural network
    x - tensor of the input values
    w's - tensors of the weights
    b's - tensors of the biases
    """
    z1 = (w11 * x + b11)
    a1 = t.relu(z1)

    z2 = (w12 * x + b12)
    a2 = t.relu(z2)

    y_a = ((w21 * a1 + b21) + (w22 * a2 + b22))

    return y_a

Define a function to update the weights and biases of the neural network

def update(w11, w12, w21, w22, b11, b12, b21, b22, lr):
    """
    This is a function to update the weights and biases
    w's - tensors of the weights
    b's - tensors of the biases
    lr - learning rate
    """
    with t.no_grad(): 
        w11.data = w11.data - lr * w11.grad
        w12.data = w12.data - lr * w12.grad
        w21.data = w21.data - lr * w21.grad
        w22.data = w22.data - lr * w22.grad

        b11.data = b11.data - lr * b11.grad
        b12.data = b12.data - lr * b12.grad
        b21.data = b21.data - lr * b21.grad
        b22.data = b22.data - lr * b22.grad

        w11.grad = None
        w12.grad = None
        w21.grad = None
        w22.grad = None

        b11.grad = None
        b12.grad = None
        b21.grad = None
        b22.grad = None

Initialise the weights and biases of the neural network using the function defined above

w11, w12, w21, w22, b11, b12, b21, b22 = init(4)

learning_rate = 0.0001

losses = []

The training loop

for i in range(5000):
    y_hat = forward(x, w11, w12, w21, w22, b11, b12, b21, b22)

    l = loss_function(y, y_hat)

    if i % 100 == 0:
        print(f"{i} loss: {l}")

    losses.append(l.item())

    l.backward()

    update(w11, w12, w21, w22, b11, b12, b21, b22, learning_rate)

0 loss: 18146.724609375
100 loss: 17325.158203125
200 loss: 16566.048828125
300 loss: 15864.330078125
400 loss: 15215.2763671875
500 loss: 14614.3701171875
600 loss: 14059.6376953125
700 loss: 13539.69921875
800 loss: 13057.98046875
900 loss: 12621.3408203125
1000 loss: 12228.5888671875
1100 loss: 11874.443359375
1200 loss: 11518.40234375
1300 loss: 11176.8154296875
1400 loss: 10938.560546875
1500 loss: 10670.21484375
1600 loss: 10421.8212890625
1700 loss: 10191.587890625
1800 loss: 9977.515625
1900 loss: 9777.203125
2000 loss: 9585.6025390625
2100 loss: 9353.912109375
2200 loss: 9293.064453125
2300 loss: 9151.208984375
2400 loss: 9019.9296875
2500 loss: 8898.3017578125
2600 loss: 8785.64453125
2700 loss: 8681.0166015625
2800 loss: 8583.7978515625
2900 loss: 8493.26953125
3000 loss: 8408.634765625
3100 loss: 8329.064453125
3200 loss: 8253.6796875
3300 loss: 8181.3232421875
3400 loss: 8109.97802734375
3500 loss: 8035.09228515625
3600 loss: 7939.9716796875
3700 loss: 7893.9365234375
3800 loss: 7717.38134765625
3900 loss: 7904.77294921875
4000 loss: 7867.05322265625
4100 loss: 7831.99951171875
4200 loss: 7799.40380859375
4300 loss: 7768.7890625
4400 loss: 7740.0087890625
4500 loss: 7713.1259765625
4600 loss: 7687.9921875
4700 loss: 7664.46337890625
4800 loss: 7641.94189453125
4900 loss: 7620.52880859375

Plot the losses to see how the model is learning

plt.plot(losses)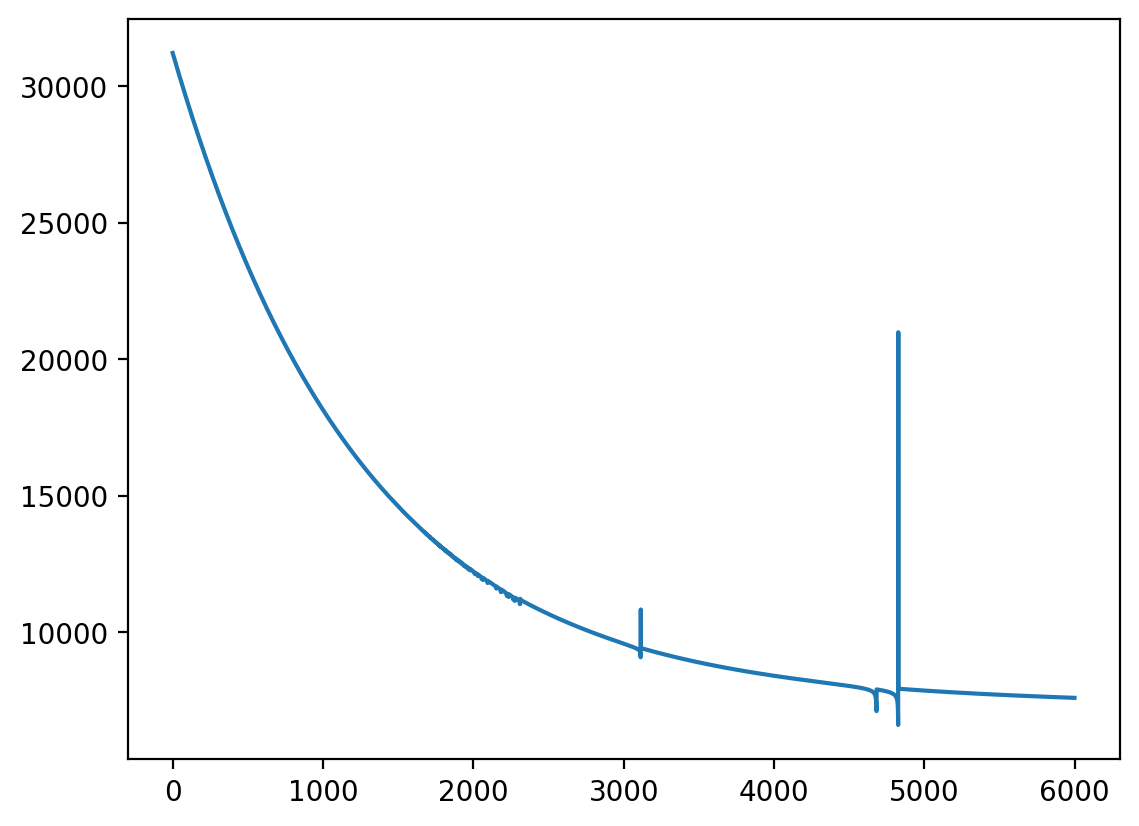

Plot the model predictions against the actual data and the function used to generate the data

graph(y_hat)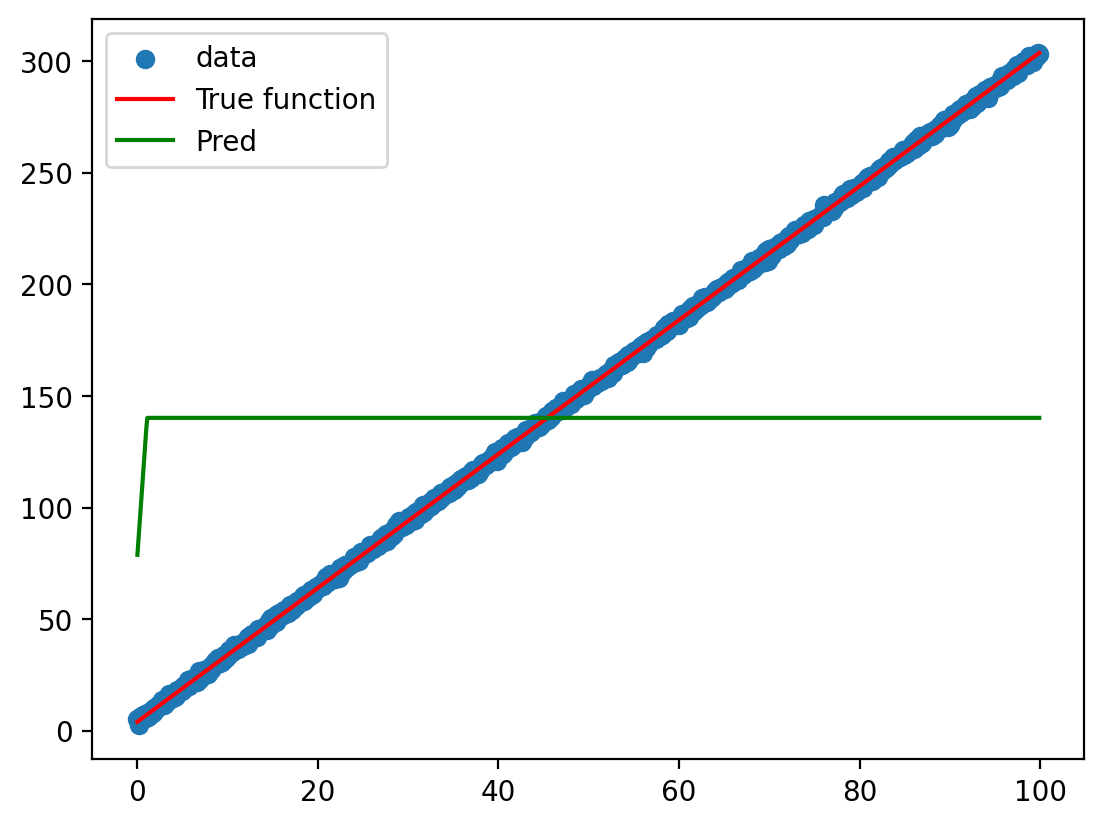

Version 3

Define a function to initialise the weights and biases of the neural network by giving the tuple of the number of neurons in each layer

def init(weight_bias_no):
    """
    This is a function to initialize the weights and biases
    weight_bias_no - list of number of neurons in each layer (inclusive of input and output layers)
    """
    weights = []
    biases = []

    for i in range(len(weight_bias_no)-1):
        weights.append(t.randn((weight_bias_no[i+1], weight_bias_no[i]), requires_grad=True, dtype=t.float32))
        biases.append(t.randn((weight_bias_no[i+1], 1), requires_grad=True, dtype=t.float32))
    
    biases[-1].data = biases[-1].data + 50.0
    # biases[-1]= t.tensor(50.0, requires_grad=True).reshape(1, 1)
    
    return weights, biases

Define a forward propagation function to calculate the predictions of the neural network

def forward(x, weights, biases):
    """
    This is a function for forward propagation of the neural network
    x - tensor of the input values
    weights - list of tensors of the weights
    biases - list of tensors of the biases
    """
    z = []
    a = [x]
    n = len(weights)

    for i in range(n-1):
        z.append(t.matmul(a[i], weights[i].t()) + biases[i].t())
        a.append(t.relu(z[i]))
    
    y_a = t.matmul(a[-1], weights[-1].t()) + biases[-1].t()

    return y_a

define a function to update the weights and biases of the neural network

def update(weights, biases, lr):
    """
    This is a function to update the weights and biases
    weights - list of tensors of the weights
    biases - list of tensors of the biases
    lr - learning rate
    """
    with t.no_grad():
        for weight in weights:
            weight.data -= lr * weight.grad
            weight.grad = None
        
        for bias in biases:
            bias.data -= lr * bias.grad
            bias.grad = None

Initialise the weights and biases of the neural network using the function defined above

weights, biases = init((1, 2, 1))

learning_rate = 0.0001

losses = []

biases

[tensor([[1.0925],
         [0.3252]], requires_grad=True),
 tensor([[49.7538]], requires_grad=True)]

The training loop

for i in range(5000):
    y_hat = forward(x, weights, biases)

    l = loss_function(y, y_hat)

    if i % 100 == 0:
        print(f"{i} loss: {l}")

    losses.append(l.item())

    l.backward()

    update(weights, biases, learning_rate)

0 loss: 4515.20654296875
100 loss: 4535.76318359375
200 loss: 4506.70068359375
300 loss: 3637.81005859375
400 loss: 3368.2919921875
500 loss: 3204.014404296875
600 loss: 3445.580078125
700 loss: 4253.38623046875
800 loss: 3140.37646484375
900 loss: 4244.9658203125
1000 loss: 4079.053466796875
1100 loss: 4532.0439453125
1200 loss: 4620.88623046875
1300 loss: 4317.896484375
1400 loss: 3441.9462890625
1500 loss: 4141.67138671875
1600 loss: 3139.8232421875
1700 loss: 3691.132080078125
1800 loss: 2773.3857421875
1900 loss: 3806.115966796875
2000 loss: 3101.822998046875
2100 loss: 2741.623046875
2200 loss: 3941.86767578125
2300 loss: 2719.452880859375
2400 loss: 2755.082763671875
2500 loss: 4121.7626953125
2600 loss: 2905.007568359375
2700 loss: 3547.77685546875
2800 loss: 2557.123291015625
2900 loss: 2638.226318359375
3000 loss: 4042.74951171875
3100 loss: 2741.59326171875
3200 loss: 2770.77783203125
3300 loss: 3632.086669921875
3400 loss: 2410.451416015625
3500 loss: 2429.709228515625
3600 loss: 3392.62451171875
3700 loss: 2638.08544921875
3800 loss: 3924.790283203125
3900 loss: 2252.53564453125
4000 loss: 3356.621337890625
4100 loss: 3026.0625
4200 loss: 3817.87548828125
4300 loss: 2254.858642578125
4400 loss: 2448.4951171875
4500 loss: 2325.39892578125
4600 loss: 2432.696044921875
4700 loss: 2453.68701171875
4800 loss: 2998.777099609375
4900 loss: 2297.80517578125

Plot the losses to see how the model is learning

plt.plot(losses)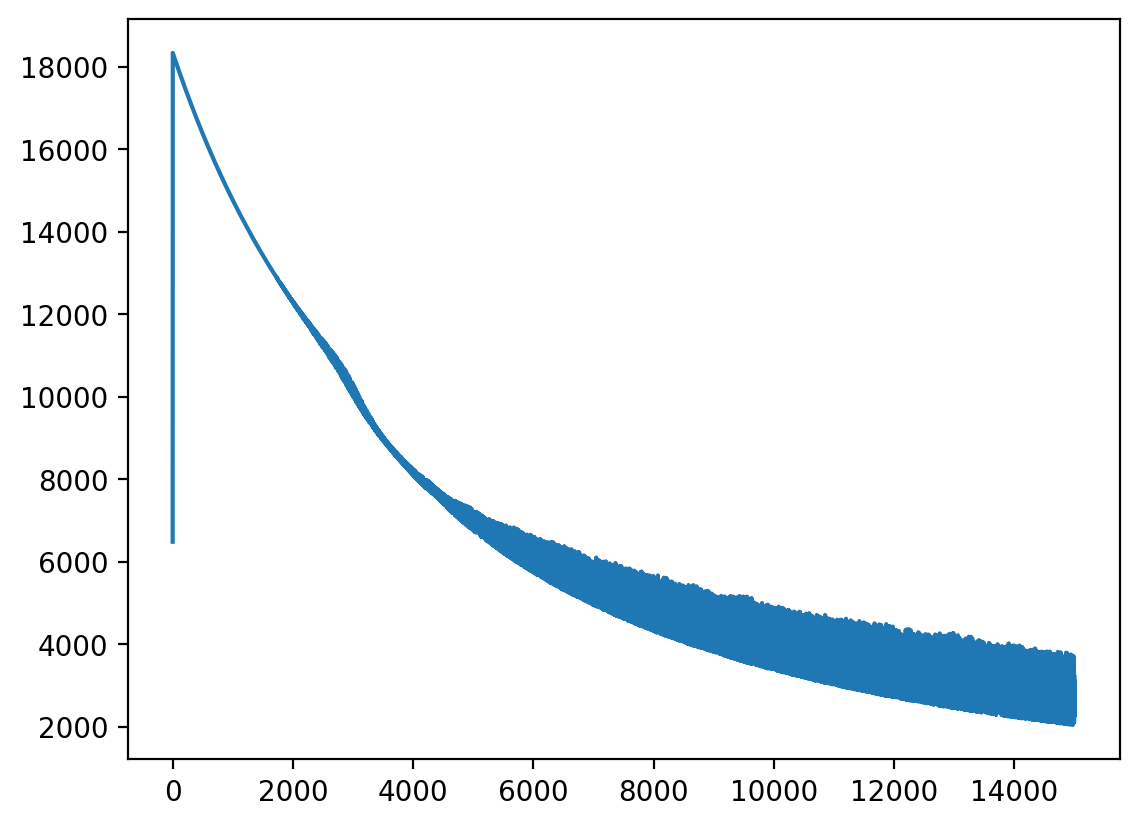

Plot the model predictions against the actual data and the function used to generate the data

graph(y_hat)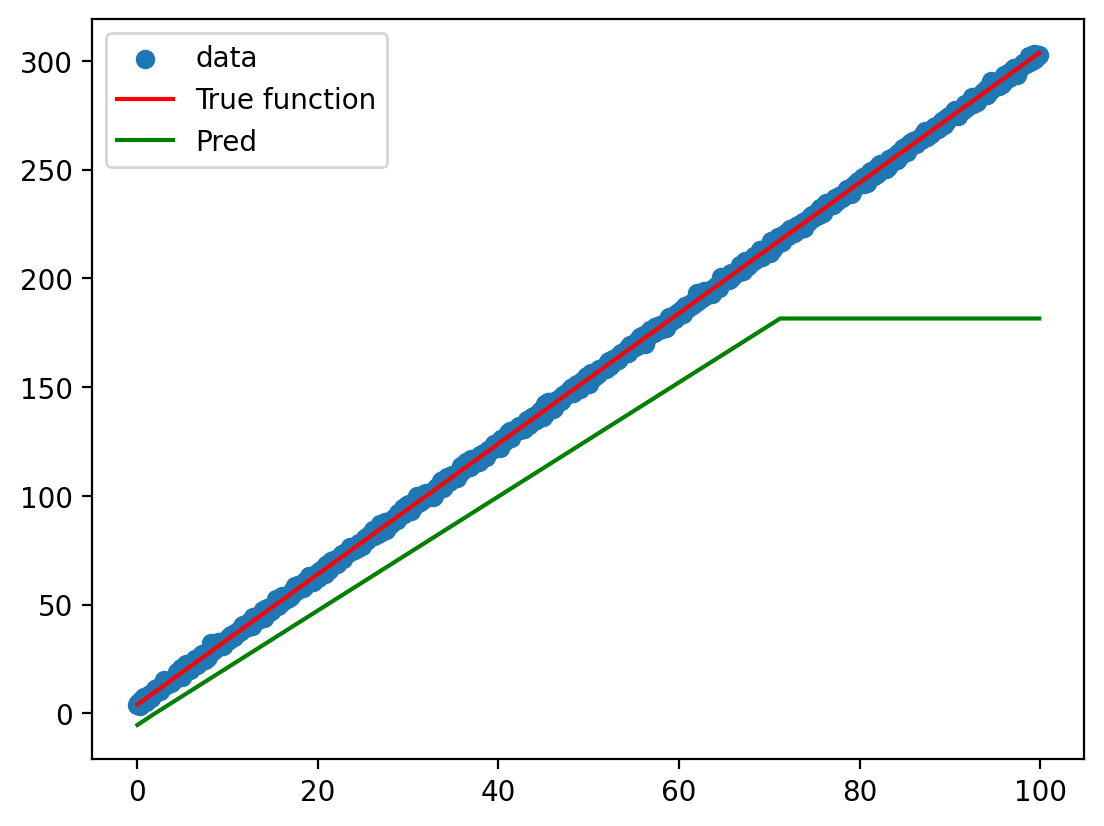

Version 4

Import some more libraries

from torch import nn
from torch.nn.modules.activation import ReLU
import torch.optim as optim

Initialise the neural network using the nn.Sequential() function with Linear layers having standard normal distribution weights and biases

l1 = nn.Linear(1, 2)
l2 = nn.Linear(2, 1)

nn.init.normal_(l1.weight, mean=0, std=1.0)
nn.init.normal_(l2.weight, mean=0, std=1.0)

# model = nn.Sequential(l1, l2)
model = nn.Sequential(l1, nn.ReLU(), l2)

model.to("cpu")

Sequential(
  (0): Linear(in_features=1, out_features=2, bias=True)
  (1): ReLU()
  (2): Linear(in_features=2, out_features=1, bias=True)
)

Define the loss function and the optimiser

list(model.named_parameters())

[('0.weight',
  Parameter containing:
  tensor([[1.4601],
          [1.0118]], requires_grad=True)),
 ('0.bias',
  Parameter containing:
  tensor([1.9046, 0.3194], requires_grad=True)),
 ('2.weight',
  Parameter containing:
  tensor([[ 2.3503, -0.4414]], requires_grad=True)),
 ('2.bias',
  Parameter containing:
  tensor([0.6655], requires_grad=True))]

# criterion = nn.MSELoss()

optimizer = optim.Adam(model.parameters(), lr = 0.001)

# losses = []

The training loop

x.shape, model(x).shape

(torch.Size([1000, 1]), torch.Size([1000, 1]))

y_hat_untrained = model(x)
graph(y_hat_untrained.ravel())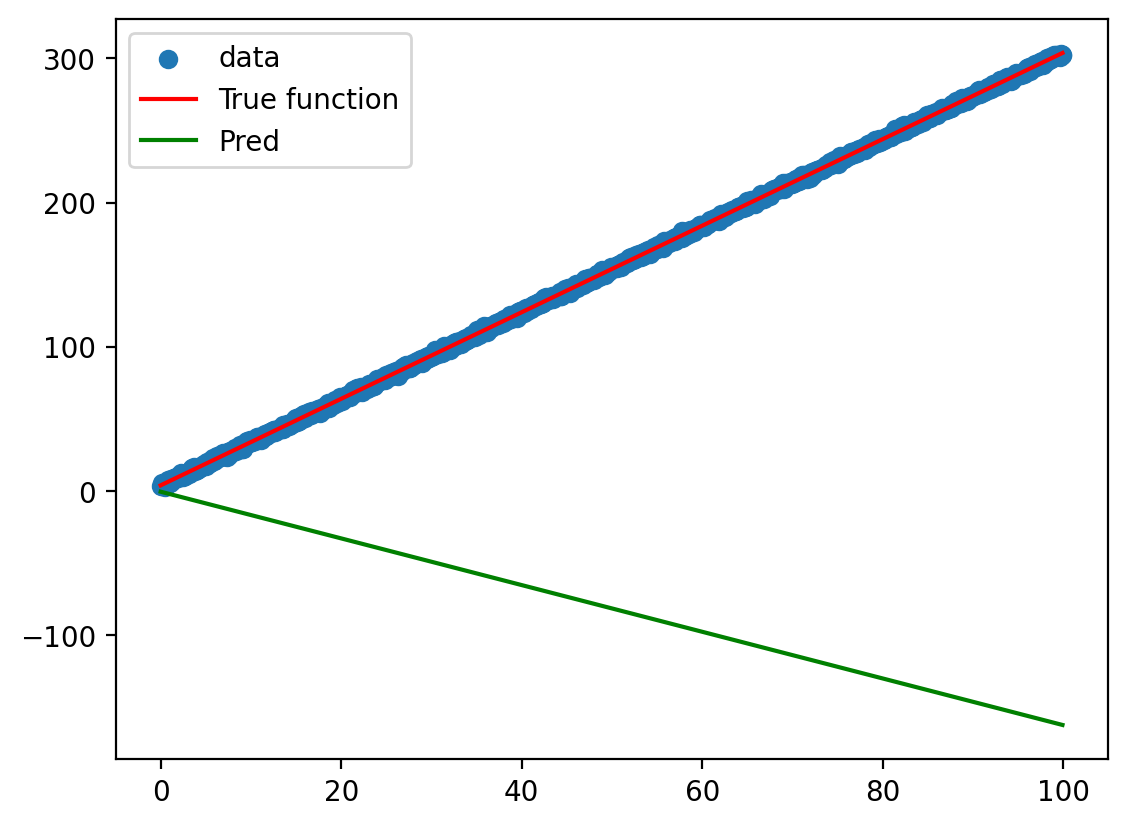

losses = []
for epoch in range(5000):
    y_hat = model(x)
    #print(y_hat.shape, y.shape)

    loss = loss_function(y_hat.ravel(), y.ravel())

    losses.append(loss.item())

    model.zero_grad()

    loss.backward()

    optimizer.step()

    if epoch % 100 == 0:
        print(f"{epoch} loss: {loss}")

0 loss: 73045.3671875
100 loss: 59914.609375
200 loss: 48524.359375
300 loss: 38676.04296875
400 loss: 30224.716796875
500 loss: 23067.9453125
600 loss: 17122.388671875
700 loss: 12305.6337890625
800 loss: 8523.5107421875
900 loss: 5663.18310546875
1000 loss: 3592.715576171875
1100 loss: 2166.874755859375
1200 loss: 1237.8662109375
1300 loss: 667.8623657226562
1400 loss: 339.697021484375
1500 loss: 162.83676147460938
1600 loss: 73.73493957519531
1700 loss: 31.79436492919922
1800 loss: 13.35311222076416
1900 loss: 5.781553745269775
2000 loss: 2.879981279373169
2100 loss: 1.843165397644043
2200 loss: 1.4977456331253052
2300 loss: 1.3902883529663086
2400 loss: 1.358534574508667
2500 loss: 1.3490084409713745
2600 loss: 1.3454464673995972
2700 loss: 1.3432934284210205
2800 loss: 1.3414008617401123
2900 loss: 1.3394927978515625
3000 loss: 1.3375006914138794
3100 loss: 1.3354159593582153
3200 loss: 1.3332253694534302
3300 loss: 1.330932855606079
3400 loss: 1.328535795211792
3500 loss: 1.32603120803833
3600 loss: 1.3234118223190308
3700 loss: 1.3206785917282104
3800 loss: 1.31782865524292
3900 loss: 1.3148642778396606
4000 loss: 1.3117693662643433
4100 loss: 1.3085378408432007
4200 loss: 1.3051718473434448
4300 loss: 1.3016676902770996
4400 loss: 1.2980235815048218
4500 loss: 1.2942390441894531
4600 loss: 1.2903125286102295
4700 loss: 1.286239504814148
4800 loss: 1.282008409500122
4900 loss: 1.2776236534118652

Plot the losses to see how the model is learning

plt.plot(losses)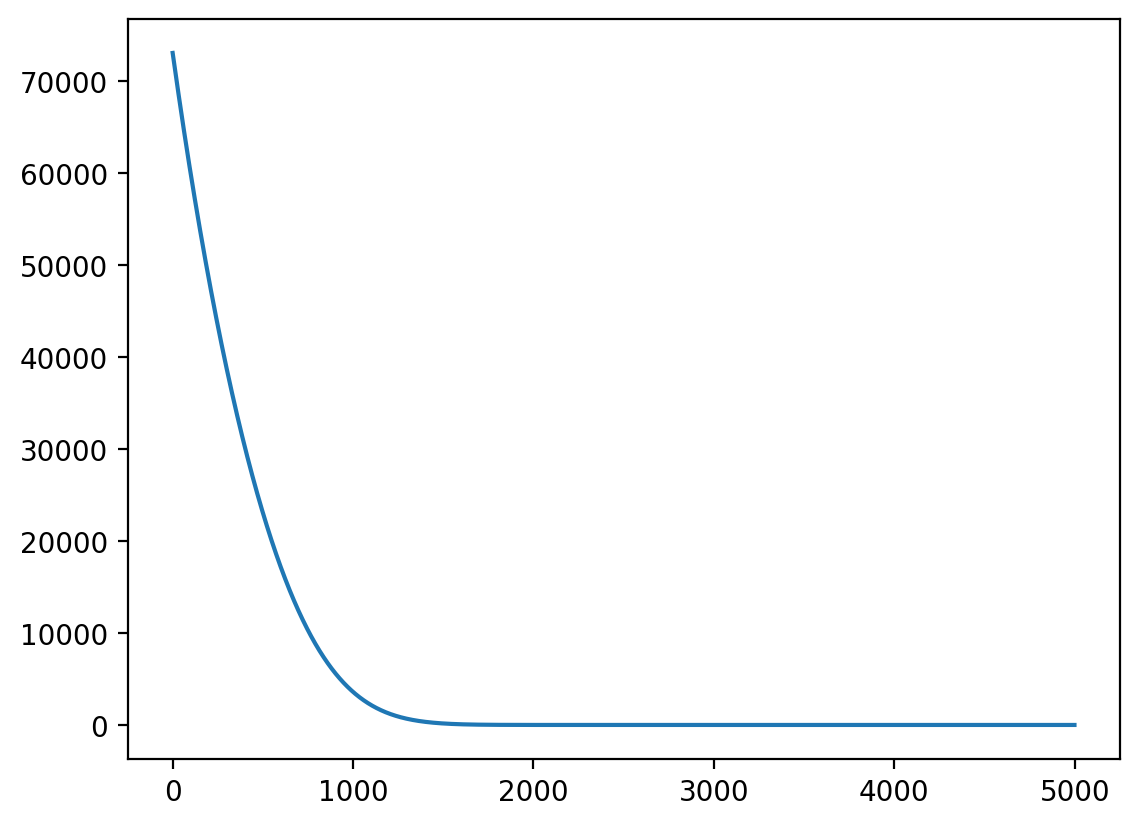

Plot the predictions of the model against the actual data and the function used to generate the data

y_hat = model(x)
graph(y_hat.ravel())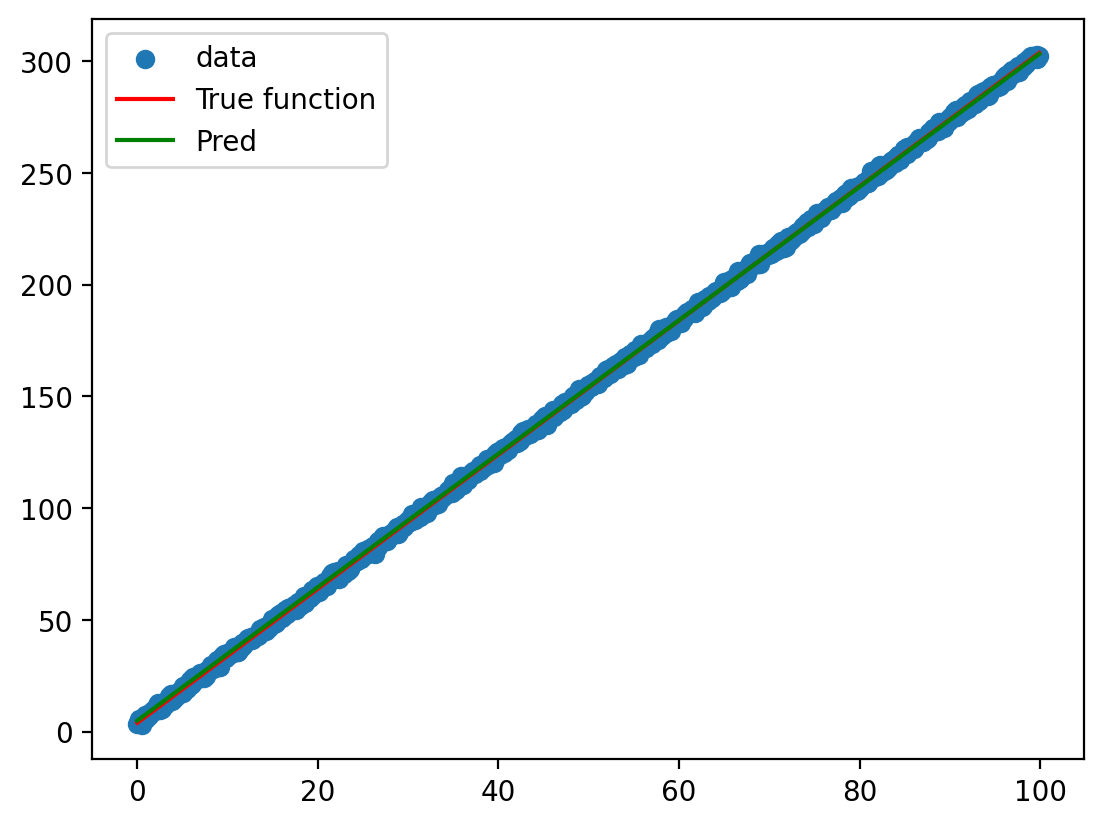

Extra

a = t.arange(1, 9)

a

tensor([1, 2, 3, 4, 5, 6, 7, 8])

a.shape

torch.Size([8])

a.reshape(4, 2)

tensor([[1, 2],
        [3, 4],
        [5, 6],
        [7, 8]])

a

tensor([1, 2, 3, 4, 5, 6, 7, 8])

a.reshape(4, 2).t()

tensor([[1, 3, 5, 7],
        [2, 4, 6, 8]])

#view, permute, ravel
#watch videos (done)
#init argument as number of layers (done)
#Version 4 with NN.linear (done)