@kullback_leibler.RegisterKL(Normal, Normal)
def _kl_normal_normal(a, b, name=None):
"""Calculate the batched KL divergence KL(a || b) with a and b Normal.
Args:
a: instance of a Normal distribution object.
b: instance of a Normal distribution object.
name: Name to use for created operations.
Default value: `None` (i.e., `'kl_normal_normal'`).
Returns:
kl_div: Batchwise KL(a || b)
"""
with tf.name_scope(name or 'kl_normal_normal'):
b_scale = tf.convert_to_tensor(b.scale) # We'll read it thrice.
diff_log_scale = tf.math.log(a.scale) - tf.math.log(b_scale)
return (
0.5 * tf.math.squared_difference(a.loc / b_scale, b.loc / b_scale) +
0.5 * tf.math.expm1(2. * diff_log_scale) -
diff_log_scale)KL-Divergence
Introduction to KL-Divergence
In this blog we want to discuss about the “KL-Divergence”. But first, we need to understand what is “distance”.
Distance
Distance is a measure of how much two objects are different.
Take two scalers \(x\) and \(y\). The distance between them is \(|x-y|\). For example, the distance between \(3\) and \(5\) is \(|3-5|=2\).
Similarly, the distance between two vectors \(\mathbf{x}\) and \(\mathbf{y}\) is \(||\mathbf{x}-\mathbf{y}||\). For example, the distance between \((1,2)\) and \((3,4)\) \[||(1,2)-(3,4)||=||(-2,-2)||=\sqrt{(-2)^2+(-2)^2}=\sqrt{8}\approx 2.83\]
Distance between two distributions
But what about the distance between two distributions \(P\) and \(Q\)? For example, two Bernoullie Distribution \(P\) and \(Q\) of probabilities of Heads & Tails on two different coins (One fair-coin and the other unbalanced). Say, \(P=[0.5, 0.5]\) and \(Q=[0.3,0.7]\)?
We can use the same formula \(||P-Q||\). \[||P-Q||=||[0.5,0.5]-[0.3,0.7]||=||[0.2,-0.2]||=\sqrt{0.2^2+(-0.2)^2}=\sqrt{0.08}\]
But this formula is not good enough for cases when we wish to measure the change in the distribution over time. i.e., how much is one distribution changed to another distribution. For example, if \(P\) is the distribution of the weather in the monsoon and \(Q\) is the distribution of the weather in the winter, then \(||P-Q||\) is not a good measure of the change in the weather. Because the change in the weather of the monsoon to the winter is not the same as the change in the weather of the winter to the monsoon.
Look at the example below:
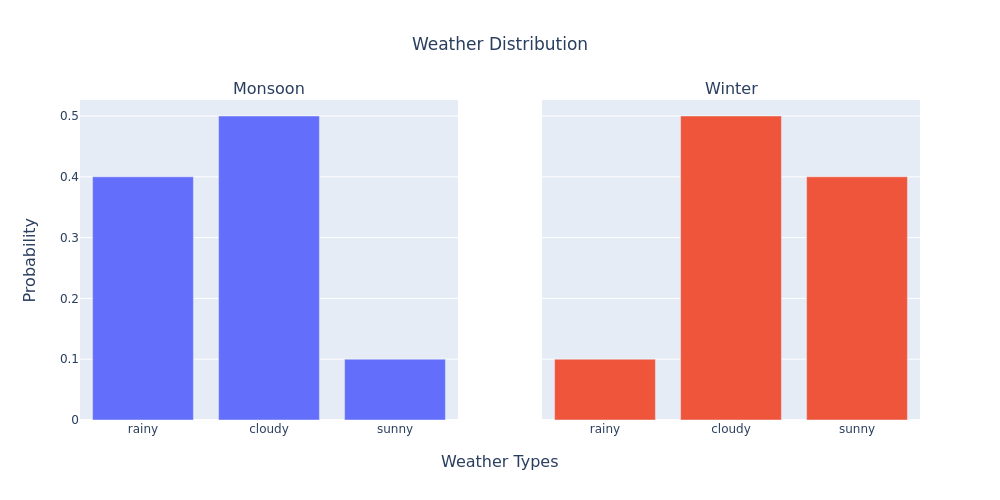
Building a better distance measure
We will try to find a better formula for the distance between two distributions
The relative change from the monsoon to the winter is:
\[\begin{align*} &\mathrm{relative\space change\space in\space rainy:\space} &\dfrac{P(\mathrm{rainy})}{Q(\mathrm{rainy})}&= \dfrac{0.1}{0.4} &= \dfrac{1}{4} &= 0.25\\ &\mathrm{relative\space change\space in\space cloudy:\space} &\dfrac{P(\mathrm{cloudy})}{Q(\mathrm{cloudy})}&= \dfrac{0.5}{0.5} &= \dfrac{5}{5} &= 1\\ &\mathrm{relative\space change\space in\space sunny:\space} &\dfrac{P(\mathrm{sunny})}{Q(\mathrm{sunny})}&= \dfrac{0.4}{0.1} &= \dfrac{4}{1} &= 4\\ \end{align*}\]
\[\mathrm{average\space relative\space change\space from\space monsoon\space to\space winter:}\]
\[\begin{align*} &= \dfrac{1}{3}\left(\dfrac{1}{4}+1+4\right)\\ &= \dfrac{1}{3}\left(\dfrac{1+4+16}{4}\right)\\ &= \dfrac{21}{12} \approx 1.75 \end{align*}\]
Issues with the relative change
However, this is skewed by large changes in the distribution like at the change values \(4\) and \(0.25\). We need to make the change in the distribution more balanced by finding some function \(f\) such that…
\[\begin{align*} f(4) &= y\\ f(0.25) &= -y \end{align*}\]
And in general
\[\begin{align*} f(x) &= y\\ f\left(\dfrac{1}{x}\right) &= -y \end{align*}\]
The logarithm function
This function is \(f(x)=\log(x)\). So, we take the average of the log of the relative change in the distribution.
\[\mathrm{average\space log\space relative\space change\space from\space monsoon\space to\space winter:}\]
\[\begin{align*} &= \dfrac{1}{3}\left(\log\left(\dfrac{1}{4}\right)+\log(1)+\log(4)\right)\\ &= \dfrac{1}{3}\left(\log\left(\dfrac{1}{4}\right)+\log(4)\right)\\ &= \dfrac{1}{3}\left(\log\left(\dfrac{1}{4}\times 4\right)\right)\\ &= \dfrac{1}{3}\left(\log(1)\right) = \dfrac{1}{3}\left(0\right) = 0 \end{align*}\]
Problem with average log relative change
BUT!! This is clearly wrong. Because the change in the distribution from the monsoon to the winter is definitely not \(0\). Then what is the problem and what are we missing?
The problem is that we are taking the average of the log of the relative change in the distribution. Rather, we should take the weighted average of the log of the relative change in the distribution. The weights should be the original distribution. i.e., the weights should be \(P\). But as we are already weighting it by \(P\), we don’t need to take the average. We just need to take the sum.
\[\mathrm{sum\space of\space log\space relative\space change\space from\space monsoon\space to\space winter:}\]
\[\begin{align*} &= P(\mathrm{rainy})\times\log\left(\dfrac{1}{4}\right) + P(\mathrm{cloudy})\times\log(1) + P(\mathrm{sunny})\times\log(4)\\ &= (0.1)\times\log\left(\dfrac{1}{4}\right) + (0.5)\times\log(1) + (0.4)\times\log(4)\\ &= (0.1)\times\log\left(\dfrac{1}{4}\right) + (0.5)\times(0) + (0.4)\times\log(4)\\ &= (0.1)\times\log\left(\dfrac{1}{4}\right) + 0 + (0.4)\times\log(4)\\ &= (0.1)\left(\log\left(\dfrac{1}{4}\right) + (4)\times\log(4)\right)\\ &= (0.1)\left(\log\left(\dfrac{1}{4}\right) + \log(4^4)\right)\\ &= (0.1)\left(\log\left(\dfrac{1}{4} \times (4^4)\right)\right)\\ &= (0.1)\left(\log(4^3)\right) = (0.1)\left(\log(64)\right) = \dfrac{\log(64)}{10}\\ \end{align*}\]
Hence the formula for the KL-Divergence between two distributions \(P\) and \(Q\).
The Kullback-Leibler Divergence
The KL-Divergence for discrete distributions is defined as follows:
\[D_{KL}(P||Q)=\sum P(x)\log\frac{P(x)}{Q(x)}\]
For continuous probability distributions \(P\) and \(Q\) the KL-Divergence is defined as:
\[\begin{align*} D_{KL}(P||Q) = \int P(x) \cdot \log\left(\dfrac{P(x)}{Q(x)} \right) dx \end{align*}\]
KL-Divergence between two Normal/Gaussian distributions
In the case of \(P(x)\sim N(\mu_1, \sigma_1)\) and \(Q(x)\sim N(\mu_2, \sigma_2)\), we would like to find the KL-Divergence.
\[\begin{align} = &\int P(x) \cdot \log\left(\dfrac{P(x)}{Q(x)}\right) dx\nonumber\\ = &\int P(x) \cdot \left(\log{P(x)} - \log{Q(x)}\right) dx\nonumber\\ = &\int P(x) \cdot \log{P(x)}dx - \int P(x) \cdot \log{Q(x)} dx\nonumber\\ = &\int P(x) \cdot \log{\left(\dfrac{1}{\sqrt{2\pi}\sigma_1}\cdot\exp{\left(-\dfrac{\left(x - \mu_1\right)^2}{2\sigma_1^2} \right)}\right)} dx\nonumber\\ &\quad - P(x) \cdot \log{\left(\dfrac{1}{\sqrt{2\pi}\sigma_2}\cdot\exp{\left(-\dfrac{\left(x - \mu_2\right)^2}{2\sigma_2^2} \right)}\right)} dx \end{align}\]
\[\begin{align} \text{Consider the $\log$ PDF of $N(\mu, \sigma)$:}\nonumber\\ = &\log{\left(\dfrac{1}{\sqrt{2\pi}\sigma}\cdot\exp{\left(-\dfrac{\left(x - \mu\right)^2}{2\sigma^2} \right)}\right)}\nonumber\\ = &-\dfrac{1}{2}\log(2\pi) - \log(\sigma) - \dfrac{1}{2}\left(\dfrac{x - \mu}{\sigma}\right)^2\\ \end{align}\]
We can rewrite \(D_{KL}(P||Q)\) as:
\[\begin{align} = &\int P(x) \left(-\dfrac{1}{2}\log(2\pi) - \log(\sigma_1) - \dfrac{1}{2}\left(\dfrac{x - \mu_1}{\sigma_2}\right)^2\right) dx\nonumber\\ &\quad - \int P(x) \left(-\dfrac{1}{2}\log(2\pi) - \log(\sigma_2) - \dfrac{1}{2}\left(\dfrac{x - \mu_2}{\sigma_2}\right)^2\right) dx\nonumber\\ = &-\dfrac{1}{2}\int P(x) \left(\dfrac{x-\mu_1}{\sigma_1}\right)^2 dx + \dfrac{1}{2}\int P(x)\left(\dfrac{x-\mu_2}{\sigma_2}\right)^2 dx\nonumber\\ &\quad + \int P(x) \cdot \log\left(\dfrac{\sigma_2}{\sigma_1}\right) dx\nonumber\\ = &\log\left(\dfrac{\sigma_2}{\sigma_1}\right)\int P(x)dx \nonumber - \dfrac{1}{2\sigma_1^2}\int\left(x-\mu_1\right)^2 P(x) dx\nonumber\\ &\quad + \dfrac{1}{2\sigma_2^2}\int\left(x-\mu_2\right)^2 P(x) dx\nonumber\\ = &\log\left(\dfrac{\sigma_2}{\sigma_1}\right) - \dfrac{\sigma_1^2}{2\sigma_1^2}\nonumber\\ &\quad + \dfrac{1}{2\sigma_2^2}\int\left(x-\mu_1 + \mu_1 -\mu_2\right)^2 P(x) dx\nonumber\\ = &\log\left(\dfrac{\sigma_2}{\sigma_1}\right) - \dfrac{1}{2}\nonumber\\ &\quad + \dfrac{1}{2\sigma_2^2}\int\left(x-\mu_1\right)^2 P(x) dx \nonumber\\ &\quad + \dfrac{2\left(\mu_1 - \mu_2\right)}{2\sigma_2^2}\int\left(x-\mu_1\right) P(x) dx\nonumber\\ &\quad + \dfrac{2\left(\mu_1 - \mu_2\right)^2}{2\sigma_2^2}\int P(x) dx\nonumber\\ = &\log\left(\dfrac{\sigma_2}{\sigma_1}\right) - \dfrac{1}{2} + \dfrac{\sigma_1^2}{2\sigma_2^2} + 0 + \dfrac{2\left(\mu_1 - \mu_2\right)^2}{2\sigma_2^2} \nonumber\\ D(P||Q) = &\log\left(\dfrac{\sigma_2}{\sigma_1}\right) + \dfrac{\sigma_1^2 + 2\left(\mu_1 - \mu_2\right)^2}{2\sigma_2^2} - \dfrac{1}{2} \nonumber \end{align}\]
Comparision with TensorFlow Probability (TFP)
TFP Implementation
Simplified Terms
\[\mathrm{diff\_ log\_ scale} = \log(\sigma_1) - \log(\sigma_2) = \log\left(\dfrac{\sigma_1}{\sigma_2}\right)\]
\[\mathrm{expm1(x)} = e^x - 1\]
\[\mathrm{squared\_ difference(x, y)} = (x - y)^2\]
Verifying it with our derivation
\[\begin{align*} D_{KL}(P||Q) = &\dfrac{1}{2} \cdot \left(\dfrac{\mu_1}{\sigma_2} - \dfrac{\mu_2}{\sigma_2}\right)^2\\ &\quad + \dfrac{1}{2} \cdot \left(\exp{\left(2 \times \log\left(\dfrac{\sigma_1}{\sigma_2}\right)\right)} - 1\right)\\ &\quad - \log\left(\dfrac{\sigma_1}{\sigma_2}\right)\\ = &\dfrac{1}{2} \cdot \left(\dfrac{\mu_1-\mu_2}{\sigma_2}\right)^2\\ &\quad + \dfrac{1}{2} \cdot \left(\exp{\left(\log\left(\left(\dfrac{\sigma_1}{\sigma_2}\right)^2\right)\right)} - 1\right)\\ &\quad + \log\left(\dfrac{\sigma_2}{\sigma_1}\right)\\ = &\dfrac{1}{2} \cdot \left(\dfrac{\mu_1-\mu_2}{\sigma_2}\right)^2\\ &\quad + \dfrac{1}{2} \cdot \left(\left(\dfrac{\sigma_1}{\sigma_2}\right)^2 - 1\right)\\ &\quad + \log\left(\dfrac{\sigma_2}{\sigma_1}\right)\\ = &\dfrac{1}{2} \cdot \left(\dfrac{\mu_1-\mu_2}{\sigma_2}\right)^2\\ &\quad + \dfrac{\sigma_1^2}{2\sigma_2^2} - \dfrac{1}{2}\\ &\quad + \log\left(\dfrac{\sigma_2}{\sigma_1}\right)\\ = &\dfrac{\left(\mu_1-\mu_2\right)^2}{2\sigma_2^2} + \dfrac{\sigma_1^2}{2\sigma_2^2} - \dfrac{1}{2} + \log\left(\dfrac{\sigma_2}{\sigma_1}\right)\\ D_{KL}(P||Q) = &\log\left(\dfrac{\sigma_2}{\sigma_1}\right) + \dfrac{\sigma_1^2 + \left(\mu_1-\mu_2\right)^2}{2\sigma_2^2} - \dfrac{1}{2}\\ \end{align*}\]
My Implementation
import torch
import plotly.express as pxu1, s1 = 0, 1
u2, s2 = -1, 2
x = torch.arange(-10, 10, 0.01)
P = torch.distributions.Normal(u1, s1)
Q = torch.distributions.Normal(u2, s2)fig = px.line()
fig.add_scatter(x=x, y=P.log_prob(x).exp(), name='P')
fig.add_scatter(x=x, y=Q.log_prob(x).exp(), name='Q')
fig.show()u1 = torch.tensor(u1)
s1 = torch.tensor(s1)
u2 = torch.tensor(u2)
s2 = torch.tensor(s2)
torch_klPQ = torch.distributions.kl.kl_divergence(P, Q)
torch_klQP = torch.distributions.kl.kl_divergence(Q, P)
print('KL Divergence of P with respect to Q: ', round(torch_klPQ.item(), 3))
print('KL Divergence of Q with respect to P: ', round(torch_klQP.item(), 3))
klPQ = torch.log(s2/s1) + (s1**2 + (u1-u2)**2)/(2*s2**2) - 0.5
klQP = torch.log(s1/s2) + (s2**2 + (u2-u1)**2)/(2*s1**2) - 0.5
print('KL Divergence of P with respect to Q: ', round(klPQ.item(), 3))
print('KL Divergence of Q with respect to P: ', round(klQP.item(), 3))KL Divergence of P with respect to Q: 0.443
KL Divergence of Q with respect to P: 1.307
KL Divergence of P with respect to Q: 0.443
KL Divergence of Q with respect to P: 1.307Monte-Carlo Estimation
Suppose we have a function \(f\), that is really complicated. We can evaluate \(f\), but we are interested in the integral of this function. Unfortunately for us, we can not analytically compute the integral of this function - maybe it’s just impossible, or maybe our math skills are not at a high enough level. The idea is to estimate the integral of a function, over a defined interval, only knowing the function expression. For such an aim, Monte-Carlo Integration is a technique for numerical integration using random numbers.
Example
For example, suppose we want to estimate the integral of the function \(f(x) = x^3 + x^2 - x + 2\) over the interval \([-1, 1]\). We know that the integral can be interpreted as the area below the function’s curve.
def f(x):
return x**3 + x**2 - x + 2x = torch.arange(-1, 1, 0.01)
y = f(x)
fig = px.area(x=x, y=y, labels={'x':'x', 'y':'f(x)'})
fig.show()If we take a random point \(x_i\) between a and b, we can multiply \(f(x_i)\) by \((b-a)\) to get the area of a rectangle of width \((b-a)\) and height \(f(x_i)\). The idea behind Monte-Carlo Integration is to approximate the integral value by the averaged area of rectangles computed for random picked \(x_i\).
n_mc_sample = 4
random_x = (1-(-1))*torch.rand(n_mc_sample) + (-1)
random_y = f(random_x)
X = torch.tensor([torch.arange(-1, 1, 0.01).tolist() for _ in range(n_mc_sample)])
Y = torch.tensor([[random_y[i]]*200 for i in range(n_mc_sample)])
I = []
for i in range(n_mc_sample):
x_val, y_val = round(random_x[i].item(), 3), round(random_y[i].item(), 3)
I.append(y_val)
fig = px.area(x=x, y=Y[i], labels={'x':'x', 'y':f'f(x{i})'}, title=f"x = {x_val}, y = {y_val}")
fig.add_scatter(x=x, y=y, mode='lines', name='f(x)')
fig.add_vline(x=x_val, line_width=3, line_dash="dash", line_color="green")
fig.show()
print("Answer: 2.667")
print(f"Integral: {round(sum(I)/n_mc_sample, 3)}")Answer: 2.667
Integral: 2.521By finding the area of the rectangles and averaging them, the resulting number gets closer and closer to the actual result of the integral. In fact, the rectangles which are too large compensate for the rectangles which are too small. This idea is formalized with the following formula, which is the Monte-Carlo Estimator.
Formula for Monte-Carlo Estimator
\[\int_{a}^{b}f(x)dx\approx\dfrac{1}{N}\sum_{i=1}^{N}{f(x_i)}\]
where \(N\) is the number of random points we pick, and \(x_i\) is a random point distributed uniformly between \(a\) and \(b\). The more points we pick, the more accurate the estimation will be.
Formula for Monte-Carlo Estimator of Expectation
Consider a case where \(X \sim p\) where \(p\) a probability density function of \(x\). Then, the Monte-Carlo Estimator of the expectation is defined as the following:
\[\int f(x) \cdot p(x) dx \approx \dfrac{1}{N}\sum_{i=1}^{N}{f(x_i)}\]
where \(x_i \sim p(x)\).
Implementation
n_mc_sample = 10000
xP = P.sample((n_mc_sample,))
xQ = Q.sample((n_mc_sample,))
mc_klPQ = (P.log_prob(xP) - Q.log_prob(xP)).mean()
mc_klQP = (Q.log_prob(xQ) - P.log_prob(xQ)).mean()
print('Monte Carlo KL Divergence of P with respect to Q: ', round(mc_klPQ.item(), 3))
print('Monte Carlo KL Divergence of Q with respect to P: ', round(mc_klQP.item(), 3))Monte Carlo KL Divergence of P with respect to Q: 0.427
Monte Carlo KL Divergence of Q with respect to P: 1.314As we can see, it’s fairly similar to the values we got earlier.
\[D_{KL}\left(P||Q\right) = 0.443\] \[D_{KL}\left(Q||P\right) = 1.307\]
For this sample size it was a decent estimation. Now let’s see how the estimation changes as we change the sample size.
n_mc_sample = 1000
xP = []
xQ = []
yP = []
yQ = []
for _ in range(n_mc_sample):
xP.append(P.sample().item())
xQ.append(Q.sample().item())
mc_klPQ = (P.log_prob(torch.tensor(xP)) - Q.log_prob(torch.tensor(xP))).mean()
mc_klQP = (Q.log_prob(torch.tensor(xQ)) - P.log_prob(torch.tensor(xQ))).mean()
yP.append(mc_klPQ.item())
yQ.append(mc_klQP.item())
fig = px.line(y=yP, labels={'x':'x', 'y':'KL(P||Q)'}, title=f'KL(P||Q) = {round(yP[-1], 3)}')
fig.add_hline(y=klPQ.item())
fig.show()
fig = px.line(y=yQ, labels={'x':'x', 'y':'KL(Q||P)'}, title=f'KL(Q||P) = {round(yQ[-1], 3)}')
fig.add_hline(y=klQP.item())
fig.show()Mixure Of Gaussian
Mixure Of Gaussian, as name suggests, is a mixture of multiple Gaussian distributions. It is defined as follows:
\[p(x) = \sum_{i=1}^{K}{\pi_i \cdot \mathcal{N}(x|\mu_i, \sigma_i)}\]
where \(\pi_i\) is the weight of the \(i\)-th Gaussian distribution, and \(\sum_{i=1}^{K}{\pi_i} = 1\).
For example, let us consider a mixture of two Gaussian distributions. The first Gaussian distribution has a mean of \(0\) and a standard deviation of \(1\). The second Gaussian distribution has a mean of \(5\) and a standard deviation of \(2\). The weight of the first Gaussian distribution is \(0.3\), and the weight of the second Gaussian distribution is \(0.7\). Then, the probability density function of the mixture of two Gaussian distributions is defined as follows:
\[p(x) = 0.3 \cdot \mathcal{N}(x|0, 1) + 0.7 \cdot \mathcal{N}(x|5, 2)\]
u1, s1, w1 = 0, 1, 0.3
u2, s2, w2 = 5, 2, 0.7
x = torch.arange(-5, 10, 0.01)
N1 = torch.distributions.Normal(u1, s1)
N2 = torch.distributions.Normal(u2, s2)
mix = torch.distributions.Categorical(torch.tensor((w1, w2)))
comp = torch.distributions.Normal(torch.tensor((u1, u2)), torch.tensor((s1, s2)))
gmm = torch.distributions.MixtureSameFamily(mix, comp)
yn1 = N1.log_prob(x).exp()
yn2 = N2.log_prob(x).exp()
y = gmm.log_prob(x).exp()
fig = px.line()
fig.add_scatter(x=x, y=yn1, mode="lines", name=f"N({u1}, {s1})")
fig.add_scatter(x=x, y=yn2, mode="lines", name=f"N({u2}, {s2})")
fig.add_scatter(x=x, y=y, mode="lines", name="MOG")
fig.show()KL-Divergence between Mixure of Gaussians and Gaussian
Consider that \(p\) is the mixture of two Gaussian Distributions we just saw, and \(q\) is a Gaussian Distribution with mean \(2\) and standard deviation \(1\). In this case, we can not compute the KL-Divergence analytically. However, we can estimate the KL-Divergence using Monte-Carlo Estimation.
\[D_{KL}\left(p||q\right) = \int p(x) \cdot \log\left(\dfrac{p(x)}{q(x)}\right) dx \approx \dfrac{1}{N}\sum_{i=1}^{N}{\log\left(\dfrac{p(x_i)}{q(x_i)}\right)}\]
where \(x_i \sim p(x)\).
Implementation
n_mc_sample = 10000
u1, s1, w1 = 0., 1., 0.3
u2, s2, w2 = 5., 2., 0.7
mix = torch.distributions.Categorical(torch.tensor((w1, w2)).float())
comp = torch.distributions.Normal(torch.tensor((u1, u2)), torch.tensor((s1, s2)))
P = torch.distributions.MixtureSameFamily(mix, comp)
Q = torch.distributions.Normal(2, 1)
xP = P.sample((n_mc_sample,))
xQ = Q.sample((n_mc_sample,))
mc_klPQ = (P.log_prob(xP) - Q.log_prob(xP)).mean()
mc_klQP = (Q.log_prob(xQ) - P.log_prob(xQ)).mean()
print('Monte Carlo KL Divergence of P with respect to Q: ', round(mc_klPQ.item(), 3))
print('Monte Carlo KL Divergence of Q with respect to P: ', round(mc_klQP.item(), 3))Monte Carlo KL Divergence of P with respect to Q: 3.841
Monte Carlo KL Divergence of Q with respect to P: 1.099